Definition (Keynes’ Beauty Contest Game)

This game was invented by John Maynard Keynes. Suppose that you hold a stock and the price is rising. However, you believe that the stock price is too high to be justified by the value of the company. You want to sell it, but you would like to wait until the price is as close to the peak as possible i.e. you want to get out of the market just before all the other investors do.

How will other investors act? How will you respond to that?

Definition (Stylized Version)

There was a newspaper in England, where players had to guess which picture other players would like most (guessing another person’s actions). Keynes likened investing to this, it’s not only what you think about the stock, but also what other people are thinking.

In the stylized version:

• Each player names an integer between 1 and 100
• Players move simultaneously
• The player who names the integer closest to two thirds of the average integer wins a prize, all the other players get nothing
• Ties are broken uniformly at random

What would be your strategy? What will other players do? What will you do in response?

Each player chooses their optimal response called the Nash Equilibrium

Suppose that a player believes that the average play will be $X$ (this includes their own integer). That player’s optimal strateegy is to say the closest integer to $\frac{2}{3} X$.

Since $X<100$ by definition, the optimal strategy of any player has to be no more than 67. But if $X$ is no more than 67, then the optimal strategy of any player has to be no more than $\frac{2}{3} 67$. This continues on, multiplying each guess by $\frac{2}{3}$.

If you keep iterating, you get that the unique Nash equilibrium of this game is for every player to announce 1! In this case, everyone ties and the winner is chosen at random. This is called a stable point

If you try to deviate from this answer, you’d be higher than the average and be guaranteed to lose.

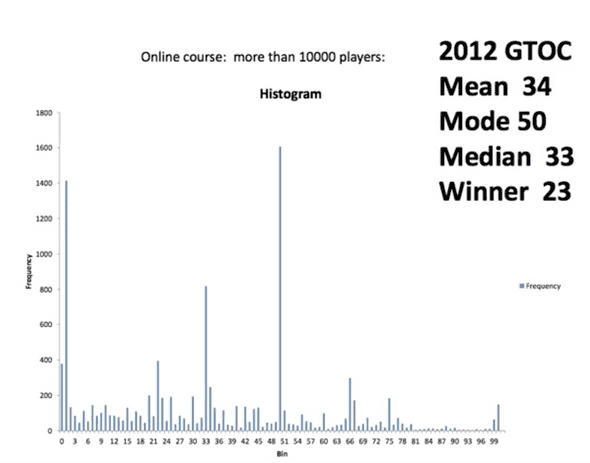
Notice that the Nash Equilibrium works if you believe that everyone can understand and reason through it. If not, you’d be better off naming a higher number.

Now suppose you get to see the results and play again. You would anticipate that everyone would shift their expectations to be lower.

In the second chance, more people move towards the equilibrium. As you increase the number of chances, the graph converges closer to the Nash Equilibrium

Definition (Nash Equilibrium)

• A consistent list of actions
• Every player’s actions maximizes his or her payoff given the actions of the others
• A self-consistent or stable game
• Each player’s action maximizes their payoff given the actions of the others
• Nobody has an incentive to deviate from their action if an equilibrium profile is played
• Someone has an incentive to deviate from a profile of actions that do not form an equilibrium

Should we expect equilibria to be played? Should we expect non-equilibria to be played?

We should expect non-equilibria to not be stable (i.e. if players see and understand it, we should expect them to move away from the equilibrium)

We saw exactly this in the second round of the game above. We should expect non-equilibria to vanish over time, but they must be learned and players must evolve.

Definition (Best Response)

If you know what everyone else will do, it will be easy to pick your own actions. Using the notation from earlier, let:

$a_{-i}=\left\langle a_{1}, \dots, a_{i-1}, a_{i+1}, \dots, a_{n}\right\rangle$

i.e. the action sequence of everyone except you (you are player $i$). Then, the entire action profile is really $a=\left(a-i, a_{i}\right)$. With this notation, the formal definition of the best response is

$a_{i}^{*} \in B R\left(a_{-i}\right) \text { iff } \forall a_{i} \in A_{i}, u_{i}\left(a_{i}^{*}, a_{-i}\right) \geq u_{i}\left(a_{i}, a_{-i}\right)$

Annotate the above

However, in reality, no agent knows what the others will do. In this case, we look for stable action profiles.

We say that $a=\left\langle a_{1}, \ldots, a_{n}\right\rangle$ is a “pure strategy” Nash Equilibrium if:

$\forall i, a_{i} \in B R\left(a_{-i}\right)$

Example (Prisoner’s Dilemma)

Suppose we have the following payoff matrix:

$\begin{array}{c|c|c|} & C & D \\ \hline C & -1,-1 & -4,0 \\ \hline D & 0,-4 & -3,-3 \\ \hline\end{array}$

This game has a dominant strategy to defect no matter what the other prisoner does. This means that the other player will do the same. Therefore $(D,D) = (-3,-3)$ is the Nash equilibrium.

Example (Two Nash Equilibria)

Suppose we have the following payoff matrix:

$\begin{array}{c|c|c|} & \text { Left } & \text { Right } \\ \text { Left } & 1,1 & 0,0 \\ \hline \text { Right } & 0,0 & 1,1 \\ \hline\end{array}$

Suppose you and another person are walking towards each other on a sidewalk. If you co-ordinate, you will be fine, but if you don’t, you will collide. In this case there are two nash equilibria: $(\text{Left},\text{Left}) = (1,1)$ and $(\text{Right},\text{Right}) = (1,1)$.

Example (Battle of the Sexes)

Suppose we have the following payoff matrix:

$\begin{array}{c|c|c} & \mathrm{B} & \mathrm{F} \\ \hline \mathrm{B} & 2,1 & 0,0 \\ \hline \mathrm{F} & 0,0 & 1,2 \\ \hline\end{array}$

Here we have two pure-strategy Nash Equilibria. If one player wants to go to $B$, the other player would be better off choosing $B$, and conversely with $F$. The best response is to go to the movie selected by the other party.

Example (Matchin Pennies)

Consider the following payoff matrix:

$\begin{array}{c|c|c|} & \text { Heads } & \text { Tails } \\ \hline \text{ Heads } & 1,-1 & -1,1\\ \hline \text { Tails } & -1,1 & 1,-1 \\ \hline\end{array}$

What is a pure strategy Nash equilibrium here? Suppose player 1 picks heads, then player 2 will pick tail. If player 2 picks tails, then player 1 will pick tails.

The best responses follow a cycle, and therefore there is NO pure strategy Nash Equilibrium here.

Built with GatsbyJS